Как быстро научиться считать в уме ребенку и взрослому

Подсчетом в уме сегодня занимается все меньше людей, потому что после появления мобильных телефонов с калькулятором намного проще и быстрее произвести все расчеты, имея под рукой гаджет. Тем не менее, любая мыслительная деятельность поддерживает организм в тонусе и замедляет процессы старения мозга, поэтому устный счет можно назвать маленькой тренировкой для мозговых структур. Данный навык имеет и практическую пользу, например, хорошо считая в уме, человек может быстро подсчитывать сдачу в магазине, поэтому его не смогут обсчитать. Любому взрослому и ребенку пригодится информация, как научиться быстро считать в уме.

Зачем считать в уме?

Грамотный устный счет можно назвать такой же незыблемой частью образования, как правописание, правильная речь или владение иностранными языками. Любой человек с базовыми представлениями об окружающем мире и искусстве должен уметь правильно считать.

Устный счет полезен по той причине, что развивает умственные способности. Он позволяет улучшать память и внимание. Человек легче концентрируется и переключается между разными потоками мышления. Подсчет в уме позволит отключиться от ненужных мыслей и переживаний. Подобные операции можно назвать своеобразной медитацией.

Если работник какой-то отрасли не знает, как быстро научиться считать деньги, то рекомендации из статьи помогут ему развить в себе необходимые способности и получить практические навыки, которые помогут его продвижению по карьерной лестнице.

Составляющие успешного обучения

Перед тем как взрослому научиться быстро считать в уме, стоит запомнить три составляющие успешного обучения, без которых не получится достичь хороших результатов:

1. Для начала нужно развивать память и уметь длительно удерживать в уме длинные числовые последовательности. Также важна концентрация внимания.
2. Полезно помнить базовые математические формулы и таблицы, которые учат в начальной и средней школе.
3. Для достижения хороших результатов в любом деле важны частые и регулярные тренировки.

Сложение в уме

Если родители не знают, как ребенку научиться быстро считать в уме, то начать стоит со сложения простых чисел. Чтобы приобрести навыки сложения больших чисел в уме, нужно научиться быстро и безошибочно складывать числовой ряд до 10, поскольку в общем процесс сложения большого слагаемого состоит из последовательности действий по суммированию простых составляющих первого десятка.

Совет! Чтобы правильно складывать, нужно владеть техникой сложения с опорой на десяток. Для этого мысленно задают вопрос, сколько единиц не хватает одному из слагаемых до десятка, а потом разность до второго слагаемого прибавляют к 10.

К примеру, при сложении 7 и 5 узнают, что для получения 10 к семерке необходимо прибавить 3. Теперь от пяти отнимают 3 и получают 2. В итоге остается прибавить к 10 полученную двойку. Получают 12. Операции выглядят так: 7+5=(7+3)+2=12.

При сложении больших слагаемых их разбивают на отдельные разряды, которые потом и складывают между собой. Допустим, нужно найти сумму 365 и 782. Первое число представляют в виде: 300+60+5, а второе будет иметь вид: 700+80+2. При сложении в уме делают следующее: (300+700)+(60+80)+(5+2)=1000+140+7=1147.

Устное вычитание чисел

Многие люди хотят знать, как быстро научиться считать сдачу. Для этого нужно уметь правильно отнимать многозначные числа. В данном случае тоже используют принцип разбивки на разряды, но делают это с тем числовым значением, которое отнимают. Например, нужно найти, сколько будет 658-215. Вычитаемое разбивают на 200+10+5. Подсчет ведут так: 658-200-10-5=458-10-5=448-5=443.

На заметку! Привычка считать в столбик немного мешает быстрому счету в уме. При вычитании удобней вести счет слева направо, разбивая на разряды.

Умножение в уме

Каждый кассир и покупатель хочет знать, как научиться быстро считать деньги на кассе. Для этого ему пригодится опыт быстрого устного деления, умножения, сложения и вычитания. В принципе, все люди помнят со школы, что умножение является многократным сложением одного из множителей. Например, 5х6=5+5+5+5+5+5=30.

Поскольку любое умножение сложного числового значения сводится к перемножению однозначных чисел, невозможно научиться быстро множить, если не знать на зубок таблицу умножения. По этой причине ее заставляют учить всех школьников начальных классов.

Множим многозначные на однозначные числа

Для начала полезно научиться множить однозначные и многозначные комбинации. К примеру, чтобы перемножить 624 на 5, первое числовое значение разбивают на разряды и делают операцию, продвигаясь от большего к меньшему. После умножения разрядов их складывают. Действия выглядят так: 624=600+20+4, затем 600х5+20х5+4х5=3000+100+20=3120.

Умножение на 11

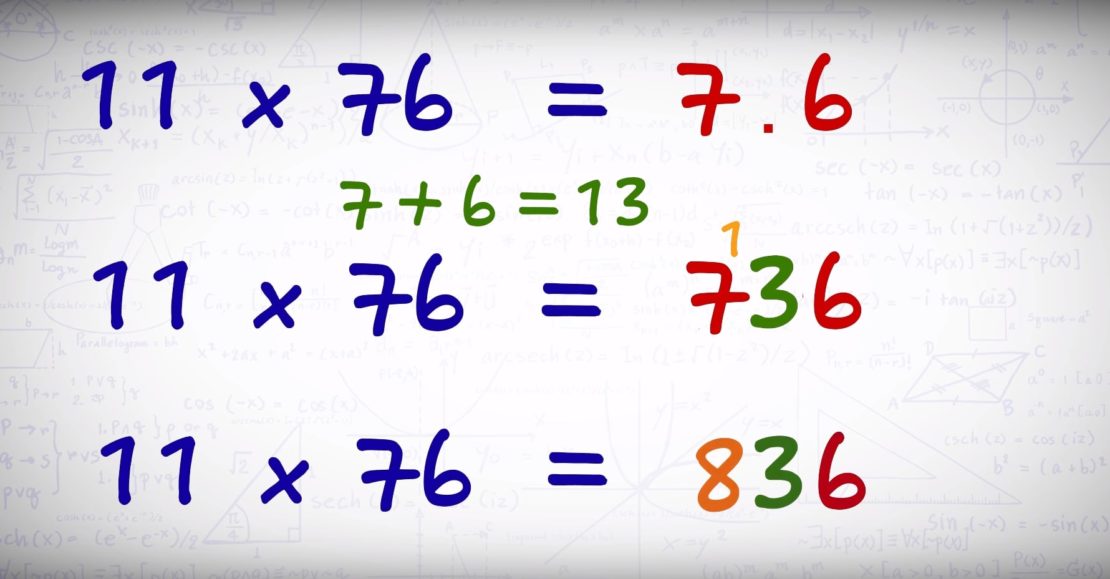
Чтобы быстро умножить любое двухзначное число на 11, используют один простой прием. Две цифры первого множителя складывают друг с другом. Полученное значение вставляют между двумя цифрами исходного числового значения. Полученная трехзначная комбинация и будет результатом вычисления. К примеру, нужно перемножить 62 и 11. Для этого делают следующее: 6+2=8. Вставив 8 между 6 и 2, получают 682. Проверяют: 62х11=682.

Если при сложении двух цифр первого множителя получается двухзначное числовое значение, то в множитель вставляют только второе число, а первое прибавляют к десяткам. Например, 75х11, 7+5=12, сначала вставляют 7(2)5, а к семерке прибавляют единицу 7+1=8, в итоге получится 825, проверяют 75х11=825.

Множим двухзначные числа

Для правильного счета важно научиться хорошо запоминать полученные комбинации, то есть возрастает нагрузка на кратковременную память. Например, нужно перемножить 45 и 28. Для этого 45 разбивают на 40+5. Далее множат как однозначные числа: 45х28=40х28+5х28=40х20+40х8+5х20+5х8=800+320+100+40=1120+140=1260.

Подсчет квадрата числа

Чтобы быстро возводить в квадрат двухзначные цифровые значения, используют еще один математический прием. Проще всего вести счет в уме с комбинациями, оканчивающимися на 5. Первую цифру нужно умножить на следующее за ней по иерархии число, то есть большее на единицу. В окончании всегда будет квадрат последней цифры. Например, нужно найти 75², подсчет ведут так: 7х8=56, 5х5=25, таким образом, 75²=75х75=5625.

Деление в уме

Отвечая на вопрос, как быстро научиться считать устно, отдельное внимание стоит уделить делению чисел. В принципе, деление является обратной операцией умножению. С делением комбинаций до ста проблемы обычно не возникают, потому при подсчете используют таблицу умножения.

Делим на однозначное число

При делении многозначного значения сначала находят его большую часть, которую несложно разделить с использованием таблицы умножения. К примеру, для деления 6144 на восемь выделяют большую часть в размере 5600, потому что ее проще всего разделить на 8. Тогда подсчет имеет вид: 6144:8=(5600+544):8=700+546:8. После этого из второго слагаемого тоже выделяют большую часть, которая легко и нацело делится на восемь: 546:8=(480+64):8=60+64:8. Разделив 64 на 8, складывают все полученные ранее результаты: 700+60+8=768.

Делим на двузначное число

При выполнении деления многозначной комбинации на двузначную цифру используют следующее правило: последняя цифра результата перемножения всегда совпадает с последним цифровым значением, полученным в результате умножения последних цифр двух этих чисел.

К примеру, необходимо умножить 1325 на 528. Согласно этому правилу, последняя цифра в результате должна быть ноль, потому что 5х8=40. Это действительно так, ведь 1325х528=699600. Теперь, удостоверившись в работе правила, можно разобраться с делением двузначного числового значения. Например, нужно найти результат деления 4424 на 56. Последовательность действий:

1. Сначала идут путем подбора, чтобы уточнить предел, в который укладывается результат. Ищут значение, которое при умножении на 56 даст число, максимально приближенное к 4424. Так, при умножении на 80 получается 4480, значит нужно брать меньшее число, но точно большее, чем 70.
2. При умножении 6 на искомую комбинацию результат должен оканчиваться на 4. Вспомнив таблицу умножения, становится понятно, что в данном случае подходит 9 и 4.
3. Таким образом, зная, что искомое значение больше 70, предполагают, что результат деления равен 79 либо 74.
4. Остается выполнить проверочное действие и перемножить комбинации. 79х56=4424. Значит, из двух чисел подходит 79. Это правильный результат деления.

Как высчитывать проценты?

Отдельно стоит рассмотреть, как быстро научиться считать проценты. Для начала нужно разобраться в значении этого слова. По сути, оно означает кусочек от сотни, которая является целой частью чего-либо. Иными словами, 8 процентов от сотни будет равно восьми, а шесть процентов от ста равно 6.

Чтобы найти 7 процентов от 300, нужно найти 7% от каждой сотни. Поскольку в 300 три сотни, получают, что семь процентов от каждой сотни равно 7, значит, 7+7+7=21. Если нужно вычислить 8 процентов от 50, то зная, что 8% от сотни равно восьми, находят 8% от 50 делением пополам, то есть результат равен 4.

Совет! Если необходимо найти процент из числа большего 100 или равного, его делят на сотни. При определении процента из комбинации меньше ста просто переносят запятую влево.

Еще один пример. Для подсчета 15 процентов от 350 делают следующее: 15+15+15+7,5=52,5. Восемь процентов от 25 равно 2, потому что при вычислении такого же процента из 250 получится 20 (8+8+4). Достаточно только передвинуть запятую вправо, чтобы узнать процент от числа 25.

Полезные рекомендации

Чтобы постоянно тренироваться в устном счете и не придумывать себе примеры, достаточно скачать мобильное приложение. Существует много методичек по ведению устного счета. В них описаны разные техники. Стоит опробовать несколько вариантов, чтобы выбрать подходящую методику, которую удобно использовать в повседневной жизни.

Также в процессе вычислений можно применять следующие полезные советы:

• • Чтобы быстро отнять от любого числа 9, достаточно вычесть из него 10 и прибавить один. Аналогично поступают при отнимании восьми, только прибавляют в этом случае 2. При вычитании семерки отнимают 10, а прибавляют три.
  • Если нужно быстро умножить на 9, то к исходному значению приписывают в конце ноль (то есть множат на 10), а потом вычитают из результата само число. Например, 75х9=750-75=675.
  • Чтобы легко и быстро умножить сложную цифровую комбинацию на 2, ее округляют до более простого значения, например, 239 округляют до 240 и множат на 2, получив 480, вычитают 2, потому что единица, на которую округлили при умножении на два, дает 2. Операция выглядит так: 240х2-1х2=480-2=478.
  • При делении на два сложного цифрового значения также прибегают к округлению. Допустим, нужно разделить 198 на 2. Число округляют до 200 и делят на два, а потом отнимают 1, потому что прибавленные две единицы при делении на 2 дают 1. Получается: 198:2=200:2-2:2=100-1=99.
  • При умножении и делении на 8 и 4 не забывают, что, по сути, эти операции являются многократным делением или умножением на два. В связи с этим лучше последовательно выполнять операцию. Например, 89х4=89х2х2=178х2=356.
  • Умножение на пять напоминает деление на два. Для быстрого умножения сложной комбинации на 5, достаточно поделить ее на два и прибавить в конце ноль. Например, 88х5=88:2=44 плюс 0, то есть получится 440.

Чтобы при подсчете в уме не ошибиться, заранее определяют диапазон цифрового значения результата. Так, при умножении однозначных чисел результат никогда не будет больше 90, потому что 9 на 9 равно 81. При умножении двузначных цифр результат не может превышать 10 тысяч. Если речь идет о трехзначных множителях, то полученное значение не может превышать 1 000 000.